２．11月の課題
３．10月の解答
４．12月の授業予告
５．今後の授業スケジュール
６．お知らせ
1. 11月授業まとめ
1.0 ＜スタートアップ(全コース)＞
割愛します。
1.1 ＜プレプライマリーコース『ゆらリン』＞
割愛します。
1.2 ＜プライマリーコース『うおうさおう』＞
割愛します。
1.3 ＜ベーシックコース『ベイスピナー』＞
ロボットというより玩具(がんぐ)と呼べそうな、コマ回しマシーンです。タッチセンサーを押してコマを加速させている間は、コマが本体に留(とど)まり、加速を止(や)めた途端(とたん)、回転の勢(いきお)いで自動的にコマが飛び出るという優(すぐ)れものです。
いつものキットで、アイデア次第(しだい)ではこんなのも作れるという新鮮(しんせん)な驚(おどろ)きを感じさせます。
さて、コマ回しを成立させるメカニズムは、マシーンとコマの双方(そうほう)にあります。
マシーン側に必要なのは、できる限り高速にコマを回転させることです。本体上部に取り付けたギアLが、どえらい速さで回りますね。
どれくらい速いのでしょうか？ モーターの回転と同じでしょうか？
だったら、モーターにシャフトを一本つき刺(さ)して、ギアLを付ければ済(す)む話です。
実際は、ギアの噛(か)み合わせを工夫して、回転スピードを上げています。
これを増速(ぞうそく)といいます。写真を見てください。
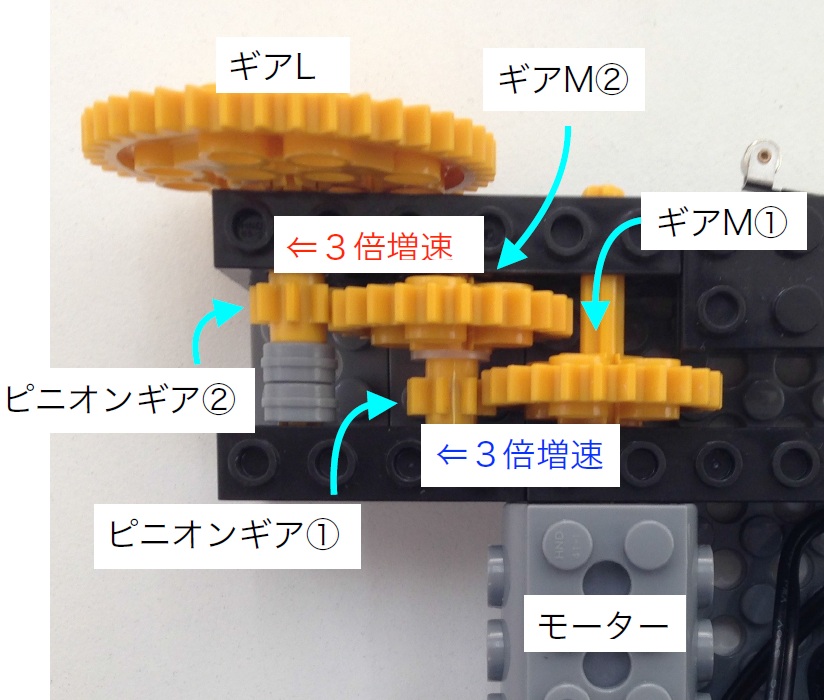〔 モーター＝ギアM① ⇒ ピニオンギア①＝ギアM② ⇒ ピニオンギア②＝ギアL 〕の順に回転を伝えていますね。
ここで、“＝”は、同一のシャフトに通して「一緒に回転している」ため、回転スピードが変わらないことを表しています。
一方、“⇒”は「大きいギアが小さいギアを回している」箇所(かしょ)であり、ここで回転スピードが上がるのです。
どれくらい上がるかは、ギアの歯数(はすう)の比(ひ)で決まります。歯数を(数字)で表すと、本体内部で、ギアM(24) ⇒ ピニオンギア(8)の３倍増速が２段と、
本体上部で、ギアL(40) ⇒ コマのギアM(24)の5/3(=1.666…)倍増速があります。
つまり、3×3×5/3＝15倍の増速作用があります。
ギアの組み替(か)え次第で、計算上はこれ以上の増速比を出せますが、今回の15倍速でも、モーターの回転速度は無負荷(むふか=空回り状態)時よりだいぶ遅(おそ)くなり、「重くしたコマの加速にも少し時間がかかる」くらいマシーンの限界能力に近いですから、これ以上に欲張(よくば)っても大差ない(*1)かもしれません。
全エネルギーをコマの回転運動に使い尽(つ)くすという意味では、とてもピュアなマシーンです。
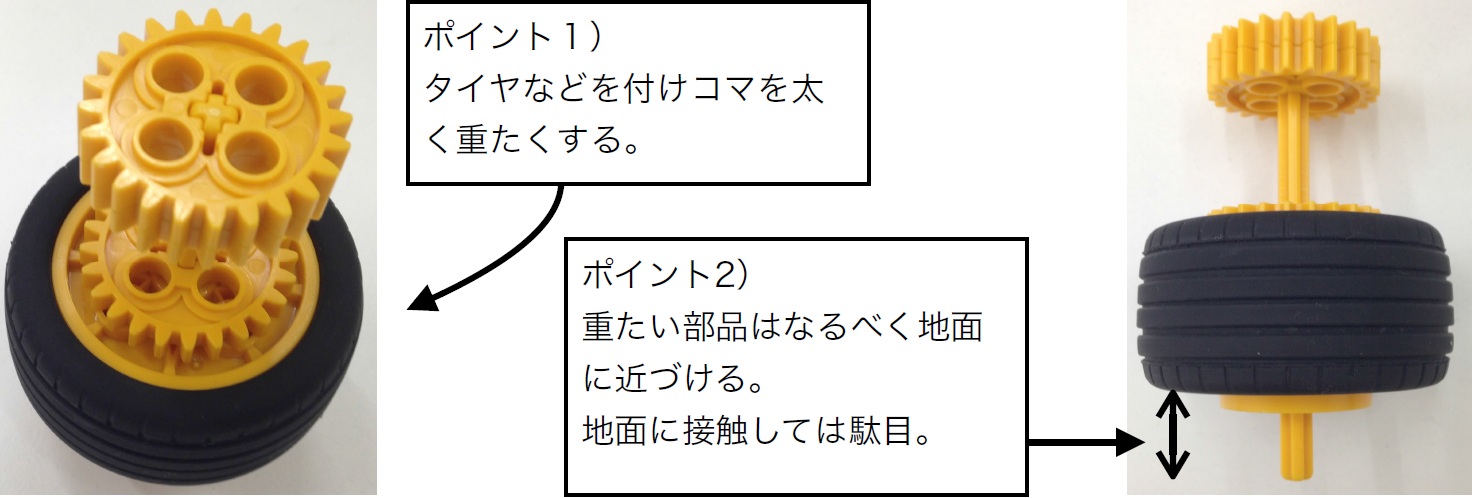
コマ側に必要なのは、いかに安定して回転が長時間続く形にするかという点です。ロボットキットの中から、軸(じく)としてシャフト、回転体として円形部品(*2)を選択するという制約下(せいやくか)では、
1) コマを重く（なるべく直径を大きく、かつ外周部を重く(*3)）
2) 重心を低く（なるべく重い部品を下の方へ(*4)）
という２点をポイントとしておきますが、
あまりに重すぎると、マシーンで十分加速できなくなったり、
あまりに低すぎると、回転中に地面に接触しやすくなったりしますので、バランスを追求する根気強さが勝負を分けます。
さて、２日目の最後に、各自のコマ回し時間を競いました。地面の材質（ザラザラの机か、ツルツルの床か）にも左右されますが、上記２点を押さえたコマなら、30秒以上回り続けることができました。
各自が試行錯誤(しこうさくご)する中で、50秒を超え、ついには1分を超えるものも登場しました。
逆に、弱かった電池をさらに消耗(しょうもう)して、最後には加速できなくなるという苦杯(くはい)をなめた人もいましたね。市販品のコマとは違って、自(みずか)ら色々と部品を組み替えて試せる点においては、遊びながら考えさせる優れた教材になったと思います。
学術的にも、コマの原理は、何年も勉強し続ける人もいるくらいとても奥深いもの。
高校物理を学んで、また改(あらた)めて興味を持ってもらえたらいいですね。
*1 限界に近いながらも、2015年5月の生徒さんが、コマ上端のギアM(24)をピニオンギア(8)に替えて、さらに3倍(トータル45倍!)の増速比を稼(かせ)いで100秒を可能にする加速方法を編(あ)み出しました。
ジェットエンジンの始動のように、加速完了まで10秒以上かけて回転音が高まるようなカッコイイもので、先生が披露すると、その方法が皆さんを虜(とりこ)にしていましたね。シリコンスプレーを吹(ふ)きかけたベイブレードスタジアム上など、低摩擦(ていまさつ)な床面(ゆかめん)であれば、120秒(2分)以上も回り続けることができました。
*2 必ずしもタイヤ・ギアのような円形部品を使う必要はなく、回転軸（シャフト）に対して対称となるような配置（点対称）なら、他の部品でも使えます。
例えば、タイヤLのホイール穴にペグを4本挿(さ)して重くした工夫例がありました。
*3 回転エネルギーをたくさん貯(た)められるようになります。このことを物理学で「慣性(かんせい)モーメントが大きい」と言います。*4 過去には、重心を高く作ったことで不利なふらつき（歳差(さいさ)運動）を、下部に履(は)かせたホイールの縁(ふち)と地面との低摩擦な接触で抑制(よくせい)し、好記録を出した工夫例も見られました。
1.4 ＜ミドルコース『ヤジロボベエ』＞
ピンと張った紐(ひも)を伝(つた)うロボットですが、１日目はロープウェイ、２日目は一輪車でサーカスの綱渡りをするようなロボットと、形態を大きく変えます。
ここまで作り変えるテーマは珍しいです。面白いですね！
学習ポイントは“重心”です。
ロープウェイ型ロボットは、ローラーだけ紐の上に掛けて、重い本体を吊(つ)り下げていますから、重心は、見た目通り、本体の中心部にあって、支点（紐と接するローラーの最下点）より下に位置します。
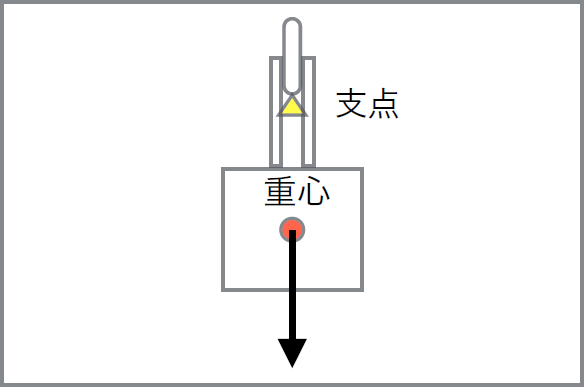重心に集中して重力が掛かると考えてよいため、（その直上の）支点も真下に引っ張られるものの、紐に引っ掛けられて（上向きの力で吊られて）いるので、安定して支えられます。ゴンドラが風に煽(あお)られて、重心が支点の真下からずれても、しばらく揺(ゆ)れるだけで、また元の安定した姿勢に収まります。
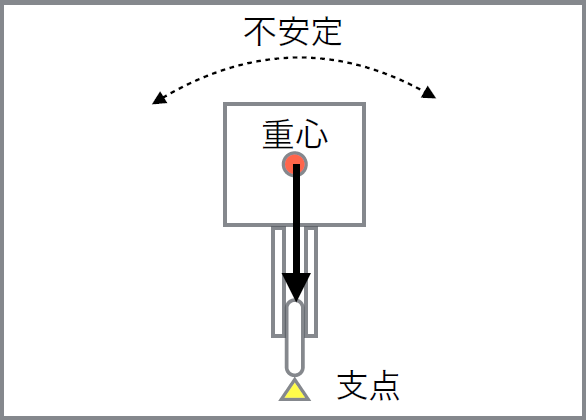ここで、このゴンドラを逆立ちさせるように、ローラーの上端を紐の上に置こうとしたら、どうなるでしょうか？支点（紐との接点）より上にきた重心が重力で引っ張られる結果、横にコロッと半回転しながら落下してしまいます。
サーカスの綱渡りもこの状態であり、本来は非常に不安定なところ、横に伸ばした両腕や長い棒を傾けつつ、上手にバランスを取っています。
このロボットに、そこまで期待できませんね。
ところが、２日目のロボット『ヤジロボベエ』は、これを見事にやってのけます。一輪車に乗った彼の重い胴体は、支点よりかなり高い位置にありそうで、逆立ちしたゴンドラ同様に不安定そうですが、なかなかどうして、バランスの取れたロボットなら、多少のロープの揺れもお構いなく、スイスイと渡ってしまいます。
なぜでしょうか？
変わったところと言えば、ハの字形をした長い棒を持っていることです。それがどうして？ 綱渡りサーカスの長い棒と同じじゃない？
いえいえ、ハの字形に垂れ下がった棒の両端に、重い電池ボックスやタイヤを取り付けているところがミソなのです。
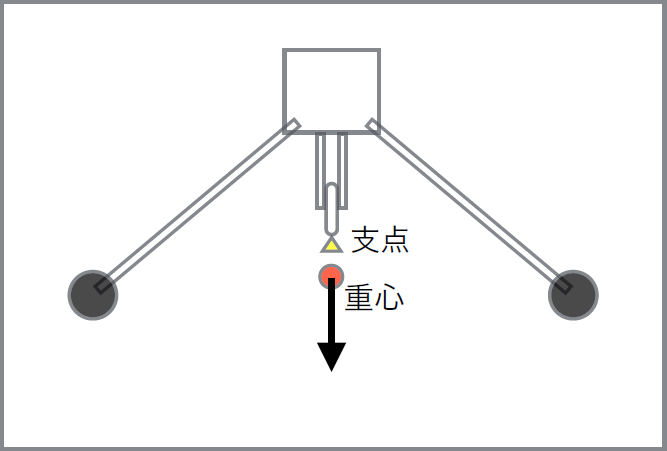これにより、ロボットの重心を支点より下に引き下げることができます。紐の真下には部品が何もないのに？ それでも構いません。
計算上、このロボットの重心は、紐の下の空中に位置することになり、これにより、彼をゴンドラ同様に安定させているのです。
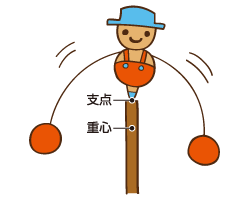
やじろべえを知っていますか？ 同じ原理です。おもりや棒の長さを調整して左右のバランスを取ることが重要ですが、それだけではありません。
一定以上に傾かず、支点もしっかり固定されているシーソーなら、左右のバランスだけ気にすればよいので、重さの代わりに支点からの長さ（座る位置）を調整してもよいのですが、足場の危(あや)ういやじろべえは、さらに、重心が支点の下にあることが必要です。
ですから、あまり棒を短くすると、重心がどんどん上がって、支点に近づくほど不安定になってしまいますので、要注意です。
皆さんのヤジロボベエは、紐の上で上手にバランスを取ることができましたか？おもりの追加や、棒の長さで調整できることは分かったと思いますが、なぜ長さの調節でもバランスが取れるのか、不思議ではありませんか？
有名な“てこの原理”ですが、おもりに働く重力（重さ）と、支点からの距離（長さ）が関係しています。
説明を簡単にするために、シーソーを使って考えてみましょう。
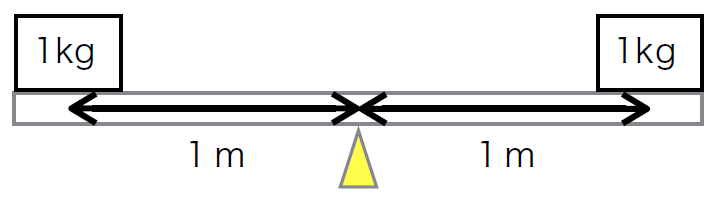図では、支点から1mの距離で、両端に1kgのおもりを置いています。この場合、左右で重さも長さも等しいので、シーソーはバランス（均衡(きんこう)状態）を取れます。
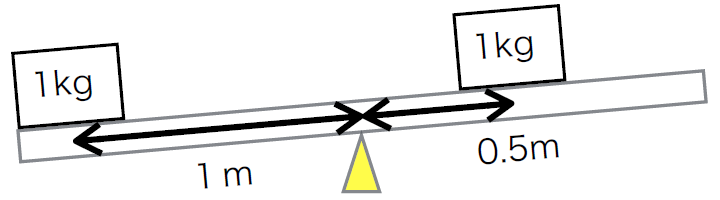次の図では、おもりの重さは変えずに、支点からの距離を右側だけ変えてみました。すると、シーソーは傾きますね。
このように、重さだけではなく、支点からおもりまでの距離によっても、支点に作用する力が変わってきます。
支点を中心に物体（シーソーの板）を回転させようとする力を回転力（トルク）と呼びます。
実は、〔 トルク ＝ 押す力(重さ) × 支点からの距離(長さ) 〕で決まります。
傾いたシーソーの支点に働くトルクを計算してみましょう。
左側のおもりによるトルク ＝ 1kg × 1m ＝ 1[kg・m] 反時計回り
右側のおもりによるトルク ＝ 1kg × 0.5m ＝ 0.5[kg・m] 時計回り
やはり、左側のトルクの方が強く、シーソーは左に傾くことが分かります。
左右のトルクを同じ（向きは逆）にすれば、シーソーはバランスを取れます。
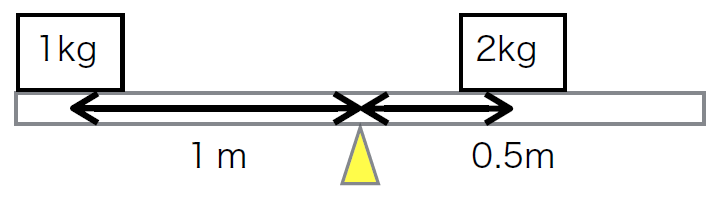最後の図ではどうでしょう。計算してみましょう。左側のおもりによるトルク ＝ 1kg × 1m ＝ 1[kg・m] 反時計回り
右側のおもりによるトルク ＝ 2kg × 0.5m ＝ 1[kg・m] 時計回り
等しくなりましたね。この場合、シーソーはバランスを取れるのです。
ヤジロボベエのバランス調整にも同じことが言えます。
おもりを付け足す代わりに、棒を長く伸ばして（おもりを支点から遠ざけて）も、トルク（傾こうとする力）を増やすことができるのです。
1.5 ＜アドバンスコース『ドレミボット②』＞
《下記を参照下さい》
https://robocobo.sakura.ne.jp/blog/robot/adv1-1711.pdf
《木琴演奏ロボットを“魔改造”した模様…》
ドレミボットは光センサーでエンコーダシート（白黒の縞模様）を読み取るので、鍵盤の位置を正しく検知できるわけですが、
プラスチック製の鍵盤を叩いてもコツコツと乾いた音がするのみで、そこから音色は出てきません。
テキストでは、叩く位置とタイミングに合わせてブザーから音を出して演奏してますが、プログラム入力の手間が大変な割に、漂(ただよ)うフェイク感が残念ですね…
「本物の鉄琴を鳴らしたい！」という生徒さんのアイデアで、手頃なサイズの鉄琴を叩いてみました。
鍵盤の間隔が異なるので、これに合わせたエンコーダシートも印刷しておきます。
あとは不要なブザーを取り外せば準備は完了(*1)、美しい音色の自動演奏が始まります。
使える音階も1.5オクターブに広がり、ブザーを鳴らす命令も省けて、良いことずくめの改造です。
スティックを二股にして和音のように音色を豊かにすることもできます。
総仕上げには「鉄琴を使った演奏会を～♪」と考えたことも過去にはありましたが、一部の血気盛んな男児たちがこれを拒否…
演奏するための繊細な腕を攻撃するための武器に改造し始めました！！
ということで、４回目の授業では恒例の(?)剣道試合が始まりました。
タッチスイッチ２個で手動操縦するプログラムにしたり(*2)、移動も攻撃も自律化するプログラムにして試合中の操作を禁じたり、派手なロボットも、地味なロボットも、様々に勝負を盛り上げていました。
演奏ネタより皆イキイキしていて、ちょっと気持ちが複雑…
*1 意外かもしれませんが、鍵盤の幅が変わってもプログラム変更は不要です。
エンコーダシート上で横切った白黒のセット数をカウントするプログラムなので、白黒ピッチを変えるだけで対応できます。
きらきら星では『ドドソソララソ』までが事実上限界のプログラムも、ブザー命令を省いて短くできるので、より長い演奏にも向いています。
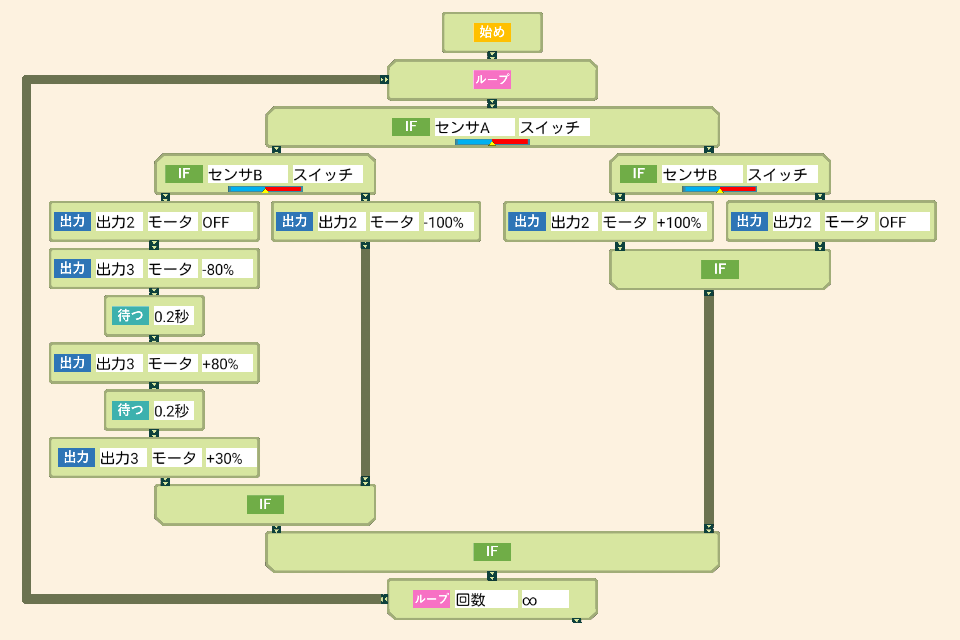
*2 タッチスイッチ２個のON/OFF（2ビット情報）で４通りの条件分岐ができますので、上図プログラムのように、打撃・左移動・右移動・停止 の４動作に割り当てます。
1.6 ＜プロ１年目コース『リンクロボット②』＞
モゾモゾ歩く多脚リンクロボットの２ヶ月目です。
前月の製作の過程で、曲線に富んだパーツをいくつも繋ぎ留めていくので、とても複雑に見えるリンク機構ですが、“節”（ジョイント部分）を直線で結んで考えれば、いくつかの変形する４節リンクを組み合わせた構造と捉えることができました。その一部のパーツ（中間リンクや従動リンク）を好きな方向に好きなだけ延長して、手足のような動きを作り出します(*1)。
４節リンクのうち、対向する２辺が等長の平行リンクでは、平行四辺形を保ちつつ整った変形を見せますが、
不等長になると、１辺（駆動リンク）を一定の速さで動かしていても、対向辺（従動リンク）では、角度によって異なる速さ(*2)で伝わったり、途中から逆回転したり、中間リンク(*3)と一直線に突っ張って動かなくなるか、回転方向が定まらずに「カクッ」と引っ掛かる状態（死点、特異点）になったりしました。
この死点または特異点は、どのリンクを駆動するかによって全く変わるので、駆動リンクと従動リンクの別に留意し、膠着(こうちゃく)状態を回避するよう設計することが重要なのでした。
ロボット教室で学習した、自動車や蒸気機関車のピストン式エンジン(*4)でも、車輪とピストンのどちらを駆動するかによって、引っ掛かりの有無が変わりましたね。
左右の脚を２個のモーターで独立して可変速度（正逆を含む）で駆動できるため、それぞれをベクトル（矢印）で表した作図により、合成された進行速度や回転中心（カーブの回転半径）が求まる考え方も学習しました。
あとは、手動（ラジコン式）プログラムだろうが、自動（タイマー式）プログラムだろうが、自律（センサー式）プログラムだろうが、左右それぞれのモーターに、どんな順序・条件・計算式で、どれくらいの数値（電圧）を与えればよいかという問題に落とし込めます。
最終月では、「感じて考える」自律型ロボットにバージョンアップしていきます。
*1 ミドルコース『ロボワン』でも学習した、てこクランク機構が基本原理です。
*2 ギアの増速・減速（てこの原理）と同様、力の大きさは反比例して伝わります。
つまり、
仕事[J = W・s] ＝ 力の大きさ[N] × 動いた距離[m]
が変わらないように、または、
仕事率[W = J/s] ＝ 力の大きさ[N] × 速度[m/s]
が変わらないように、エネルギーが伝わります。第3回テキストp.4～7参照。
*3 駆動リンクと従動リンクを繋ぐリンク。第3回テキストp.3参照。
*4 スライダークランク機構と呼ばれます。第3回テキストp.12参照。
1.7 ＜プロ２年目コース『センサーロボット②』＞
1年目のオムニホイールロボットを３つのセンサー（超音波センサー2個とカラーセンサー）で“武装”し、自分の判断で全方位に動き回れる侮れないマシンです。円らなボディーにモジャモジャ配線を這わせ、赤いデジタル数字を怪しく光らせる君は、やはり、どう見ても“爆弾”です。
センサーが多くなるにつれ、場合分け（条件分岐）の数も膨らみます。
先ずは、「どこからの情報が必要で、どんな値の時に、何をするか？」を考え、センサーの設置場所と、プログラムの流れ（フローチャート）を構築します。
次に、具体的に「このセンサーがこんな値の範囲だったら、これをして、さもなくて、あんな値だったら、あれをして…」という、条件文と行動文を記述していきます。
下記の例において、S, R, T, Mは、分岐を判断するためのパラメータ（センサー読み取り値を入れる変数）です。
int S = テストの点数;
int R = テストの順位;
int T = 現在の時刻;
int M = 持ち金;
if (S >= 80 || R < 10) { //テストが80点以上か、または9位以内だったら
迎えに来てと電話する;
} else if (T < 17) { //さもなくて(80点未満で、かつ10位以降で)、17時前なら
寄り道して帰る;
} else if (M >= 200) { //さもなくて(80点未満・10位以降・17時過ぎ)、持ち金200円以上なら
バスに乗って帰る;
} else { //さもなければ(80点未満・10位以降・17時過ぎで、持ち金も少ない)
泣きながら走って帰る;
}
長く複雑なプログラムを書く中で、決まった手順の命令群を何度も実行したい場合が多々あります。
これを“関数”として、名前を付けて定義しておけば、あとはその名前を１回呼ぶだけで複数の命令をまとめて実行してくれるので、プログラムが楽で確実なものになります。
例えば、中学２年の数学で習う一次関数 y = 2x + 3 において、x = 0, 1, 2 のときの y の値を y0, y1, y2 にそれぞれ代入するプログラムを考えます。
x0 = 0;
x1 = 1;
x2 = 2;
y0 = 2*x0 + 3; //計算式を書く
y1 = 2*x1 + 3; // また書く
y2 = 2*x2 + 3; // また書く…間違わないかな…
何度も同じような計算式を書きましたね。
これは、下記の関数定義を使った書き方もできます。
int func1(int x) { //１つの引数 x を受け取り、１つの戻り値 y を返す関数の例
int y = x*2 + 3; //ここで式を1回書くだけ
return y;
}
y0 = func1(x0); //関数を呼び出す方が楽だな…コピペしやすいし
y1 = func1(x1);
y2 = func1(x2);
関数 func1() は、数学の関数同様、戻り値を計算して返す以外に何もしませんが、逆に、内部でいろんな処理を実行して、何も値を返さない(void型)関数もあり得ます。
引数を受け取らなかったり、複数受け取ったりするようにすら定義できます(*1)。
戻り値の計算式が複雑であるほど、もしくは、まとめて実行したい命令文が多いほど、関数を使った書き方が好ましいと思えるでしょう。
さて、7セグに表示する上で、マイコンが５や８などの数字の形を特別に認識しているわけではなく、そのように見えるように光らせるセグメントのパターン情報が誰か（人間）の手によってどこかに定義されており、LEDドットマトリクスに図形を描くのと同様に制御しているに過ぎません。
だから、数字に限らず、自動販売機のルーレットのようなアニメーション表示も特別な操作ではないのです。
アニメーションのコマ毎のパターンを記憶するのに、“配列”が紹介されました。
配列は、意味的に関係のある多数の値を順番を付けて保持し、参照するのに好都合な“変数の整理箱”です。
先ほどの関数呼び出しは、次のように配列を使った書き方もできます。
int x[] = {0, 1, 2}; // x[0]=0, x[1]=1, x[2]=2 になる
int y[3]; // y[0], y[1], y[2] の３つの箱を用意
y[0] = func1(x[0]);
y[1] = func1(x[1]);
y[2] = func1(x[2]);
for文を使って代入すると、さらにシンプルにまとまります。
for (int i=0; i<3; i++) {
y[i] = func1(x[i]); // 関数呼び出しを1回書くだけで済む
}
for文と配列で、関数も不要なほどシンプルに書けることがあります。
for (int i=0; i<3; i++) {
y[i] = x[i]*2 + 3; // y = 2x + 3 の計算式を1回書くだけで済む
}
１日目の暗がりを好んで探し回ったり、好きな色を追い求めたり、２日目の迷路を探索するロボットは、どれも高度な機能で実現していますが、
特別なのは、モーター、距離センサー、色センサー、そして汎用頭脳たるマイコンなどのハードウェアと、便利に扱うための専用命令群（ソフトウェアライブラリ）であり、これらは専門の人に用意してもらわねばなりません。
しかし、その後は、上述したような判断論理をプログラムの基本構文を使って書くだけなのです。
まだ「それが難しくて大変なんだ」と言うかもしれませんが、一度やれば、次はその知識が80%活かせる世界です。英単語のように膨大に覚えることはありません。
20%ずつ新しいことを学ぶだけで、あっという間に上級者になれますよ。
*1 数学でいう関数ほど厳密な定義はなく、入力値(引数)を受け取ったり、出力値(戻り値)を返したりせず、一連の決まった処理を行うだけのものも含むので、手続き(プロシージャ)、サブルーチン、モジュールとも呼びます。
1.8 ＜プロ３年目コース『不思議アイテムIII-2②』＞
高解像度（一昔前の…）フルカラーLCD（液晶ディスプレイ）が手に入ったところで、ゲームのキャラクターでも表示したくなるのが人情です。
絵の表示には、ドット単位の画像データを作成し、プログラム内に格納し(*1)、そのデータをスキャンしながら１ドットずつ描画するルーチンを記述しなければなりません。
話を簡略化し、3×3ドット、デジタルRGB(8色)カラー画像データを格納するコードでおさらいします。
//色番号 黒=0,青=1,赤=2,紫=3,緑=4,水=5,黄=6,白=7
char B[] = {0, 255, 0, 255, 0, 255, 0, 255};
char R[] = {0, 0, 255, 255, 0, 0, 255, 255};
char G[] = {0, 0, 0, 0, 255, 255, 255, 255};
//255は最大輝度；16進数で書くと0xFF
char pic1[9] = { // １次元配列の画素データ
1, 6, 2, 1, 6, 2, 1, 6, 2
};
char pic2[3][3] = { // ２次元配列の画素データ
{1, 6, 2},
{1, 6, 2},
{1, 6, 2},
};
char pic3[3][3][3] = { // ３次元配列の画素データ
{ {255, 0, 0}, {0, 255, 255}, {0, 255, 0} },
{ {255, 0, 0}, {0, 255, 255}, {0, 255, 0} },
{ {255, 0, 0}, {0, 255, 255}, {0, 255, 0} },
};
int x, y, color1, color2;
for (y = 0; y < 3; y++) {
for (x = 0; x < 3; x++) {
// １次元配列データを描画
color1 = pic1[y*3 + x]; // pic1[0]…pic1[8]
TFT.stroke(B[color1], G[color1], R[color1]); //色設定
TFT.point(15 + x, 15 + y); // (15,15)を左上始点にドット打ち
// ２次元配列データを描画
color2 = pic2[y][x]; // pic2[0][0]…pic2[2][2]
TFT.stroke(B[color2], G[color2], R[color2]); //色設定
TFT.point(25 + x, 25 + y); // (25,25)を左上始点にドット打ち
// ３次元配列データを描画
TFT.stroke(pic3[y][x][0], pic3[y][x][2], pic3[y][x][1]); //色設定
TFT.point(35 + x, 35 + y); // (35,35)を左上始点にドット打ち
}
}
上記のプログラムでは、配列 pic1, pic2, pic3 の何れの画素データからも、同じルーマニア国旗を描きます。画像データが大きくなるほど、１次元配列 pic1 よりも、２次元配列 pic2 を使った記法の方が書くにも読むにも分かり易くなるのが分かるでしょう(*2)。
３次元配列 pic3 の記法はどうでしょうか。これなら色番号0～7毎の青・赤・緑の輝度配列 B[], R[], G[] を定義する必要もなく、各原色を256階調(*3)で直接記述できますので、オールマイティには違いありません。
しかしながら、クレヨンの8色セットがいいのか、512色セットがいいのか、1677万7216色セットがいいのかは、描く絵と技量によります。
6色だの、15色だの、表現力と処理能力の乏しさに悩んだ40年前と異なり、コンピュータが人間の感性を超えて高性能化を遂げた現代では、何でもマシンの最大能力を生かすのが最善策ではありません。
一先ず私たち素人がゲーム画面を構成するのに、8色や16色パレットを定義して扱い易くし、画像データ量も抑える上記のやり方は、優れた一例でしょう。
*1 パソコンゲームや動画再生ソフト等の大規模プログラムでは、描画プログラムとデータ部を分けて保存しますが、小規模な画像データは、プログラム内にコーディングすることもあります。
*2 pic1 へのデータ入力も、改行で工夫して pic2 への入力と遜色なく見やすく書けますが、２次元画素データは pic2[y][x] のように２次元的にアクセスできた方が圧倒的にスマートです。
*3 輝度を8ビット(1バイト)で表わすので 2の8乗＝256通り、RGB３色の組合せで 256の3乗＝2の24乗＝1677万7216色（フルカラー）を表現できます。
2. 11月の課題
＜スタートアップ(全コース)＞
特にありません
＜プレプライマリーコース＞ （プライマリーではありません）
- オリジナル図形プリント
https://robocobo.sakura.ne.jp/blog/HW/RobotPP2311-Q.pdf
＜プライマリーコース＞
- オリジナル図形プリント
https://robocobo.sakura.ne.jp/blog/HW/RobotP2311-Q.pdf
＜ベーシックコース＞
- 授業まとめを精読する（概ね３年生以上／低学年は補助の下で）
- オリジナル課題プリント（３面図＋設問）
https://robocobo.sakura.ne.jp/blog/HW/RobotB2311-Q.pdf
＜ミドルコース＞
- 授業まとめを精読する
- オリジナル課題プリント（３面図＋設問）
https://robocobo.sakura.ne.jp/blog/HW/RobotM2311-Q.pdf
＜アドバンスコース＞
- 授業まとめを精読する
- オリジナル課題プリント（見取図＋設問）
https://robocobo.sakura.ne.jp/blog/HW/RobotA2310-Q.pdf (10月配信済み)
＜プロ１年目コース＞
- 授業まとめを精読する（該当テキストページを見ながら）
＜プロ２年目コース＞
- 授業まとめを精読する（該当テキストページを見ながら）
＜プロ３年目コース＞
- 授業まとめを精読する（該当テキストページを見ながら）
-《第3回テキストp.22 ステップアップ 拡張》
[DotChara*]をベースに、必要に応じて色コードセットを変更し、
任意のサイズ・絵柄のドット絵データを作成し表示する（１日目）
3. 10月の解答
＜プレプライマリーコース＞
https://robocobo.sakura.ne.jp/blog/HW/RobotPP2310-A.pdf
＜プライマリーコース＞
https://robocobo.sakura.ne.jp/blog/HW/RobotP2310-A.pdf
＜ベーシックコース＞
https://robocobo.sakura.ne.jp/blog/HW/RobotB2310-A.pdf
＜ミドルコース＞
https://robocobo.sakura.ne.jp/blog/HW/RobotM2310-A.pdf
＜アドバンスコース＞
翌テーマ1ヶ月目(来月)に配信します
4. 12月の授業予告
https://robocobo.sakura.ne.jp/blog/hap/robo-2312.pdf＜プレプライマリーコース＞『モッテクテク』
＜プライマリーコース＞『アルペンくん』
＜ベーシックコース＞『ロボモンキー』
＜ミドルコース＞ 『チクタクロック』
＜アドバンスコース＞『アルクンダーＺ①』
＜プロ１年目コース＞『リンクロボット③』
＜プロ２年目コース＞『センサーロボット③』
＜プロ３年目コース＞『不思議アイテムIII-2③』
5. 今後の授業スケジュール
◆中間は【ハピネスなかま】での開催が多発します。
――――――――――【佐藤教室長】――――――――――
［東福間］第1・3土原則<学習ルームでこぼこ>
- 13:30～ ベーシック／プライマリ
- 15:30～ ミドル
- 17:30～ アドバンス
⇒ 12/2, 16, 1/6, 20, 2/3, 17
［東福間プロ］第2・4日原則<学習ルームでこぼこ>
- 10:00～ プロ1年目
- 13:00～ プロ2年目
- 16:00～ プロ3年目
⇒ 12/10, 24, 1/14, 28, 2/11, 25
［中間］第2・4土原則
- 13:30～ ベーシック／プライマリ
- 15:30～ ミドル
- 17:30～ アドバンス／プロ1・2・3年目
⇒12/ 9※第1回 総合会館ハピネスなかま2F和室
12/23※第2回 総合会館ハピネスなかま2F和室
1/13※, 27※, 2/10※, 24※
※来年3月まで【ハピネスなかま】での開催が多発します
［小倉北］第1・3日原則<ムーブ>
- 10:30～ ベーシック／プライマリ
- 13:00～ ミドル
- 15:00～ アドバンス
- 12:30～ プロ1年目
- 15:00～ プロ2・3年目
⇒12/ 3 第1回 5F企画ルーム1・4F茶室
12/17 第2回 5F企画ルーム1・2
1/7, 21, 2/4, 18
――――――――――【中野教室長】――――――――――
［八幡東］第1・3土原則<レインボープラザ4F>
- 13:30～ ベーシック／プライマリ
- 15:30～ ミドル
- 17:30～ アドバンス
⇒ 12/2, 16, 1/6, 20, 2/3, 17
［小倉南］第2・4日原則<総合農事センター2F>
- 10:30～ ベーシック／プライマリ
- 13:00～ ミドル
- 15:00～ アドバンス
⇒ 12/10, 24, 1/14, 28, 2/11, 25
6. お知らせ
1) 保護者様マイページ『Lynx』開始
ヒューマンアカデミー本部より、各種サービスやキャンペーン情報、全国大会やイベント告知、新サービス「ロボット教室検定」等、
ご連絡・申込みWebサイトとして、11/6(月)～Lynx(リンクス)が始動しました。
【チラシ(11月配布)】
https://robocobo.sakura.ne.jp/blog/net/Lynx_Hogosya_A4_A.pdf
Lynxでご案内する情報は、本月報から省いて参りますので、お早目にご登録下さい。
（ご兄弟姉妹や、こどもプログラミング教室など複数お通いでも、各ご家庭１アカウントで済みます）
11/30迄のご登録で、抽選で100名様に「選べるe-GIFT」1,000円分が当たります。
2) X'masツリー2023 電子工作講座 終了
11/23(木・祝)北九州パレスにて、１０名の方に参加頂きました。
自分で配色を決めた４色７本のLEDと、その点灯パターンを書き込んだマイコンなど、計24ヶ所を🎄形基板にはんだ付けしました。
２年前は３件も発生した、はんだ付け秒数が長すぎることによるLED熱破壊もなく、全員が完動品を持ち帰ることができました。
クリスマス・ディナー🍾の食卓を飾った後、イブの夜を灯し続けましょう✨
3) 10月課題 高得点者 []内は教室と学年
◆プレプライマリ【6名平均 図形3.7】
5点…高村[東福間1], 中野[東福間1]
◆プライマリ【7名平均 図形3.9】
5点…末永[小倉北2], 田村[小倉北3]
◆ベーシック【16名平均 図面3.7＋設問2.0＝5.7】
10点…なし
9点…なし
8点…亀平[八幡東2], 井上[小倉南3], 吉岡[小倉南3]
7点…林田[八幡東2], 宮尾[八幡東5], 山根[八幡東2], 関本[小倉北3]
◆ミドル【10名平均 図面2.8＋設問1.8＝4.6】
10点…なし
9点…なし
8点…なし
7点…なし
6点…福永[東福間5], 鑓水[八幡東4], 古川[小倉北4], 有松[小倉南4]
東福間・中間・小倉北教室 佐藤 / 八幡東・小倉南教室 中野
