２．今月の課題
３．今後の授業スケジュール
４．お知らせ
1. 11月授業内容
1.0 ＜スタートアップ(全コース)＞
割愛します。
1.1 ＜プライマリーコース『ロボコング』＞
割愛します。
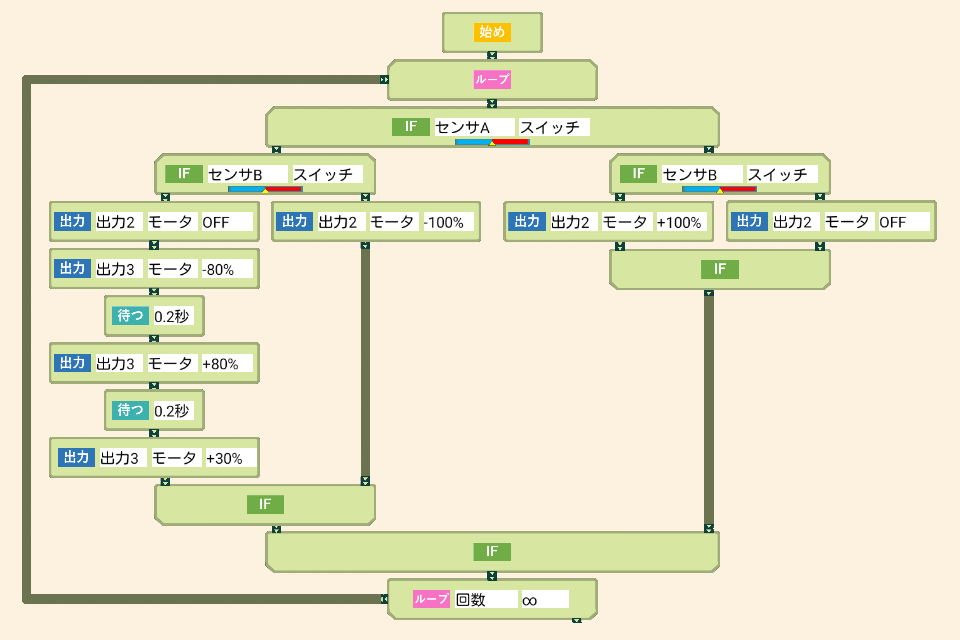
1.2 ＜ベーシックコース『ベイスピナー』＞
ロボットというより玩具(がんぐ)と呼べそうな、コマ回しマシーンです。タッチセンサーを押してコマを加速させている間は、コマが本体に留(とど)まり、加速を止(や)めた途端(とたん)、回転の勢(いきお)いで自動的にコマが飛び出るという優(すぐ)れものです。
いつものキットで、アイデア次第(しだい)ではこんなのも作れるという新鮮(しんせん)な驚(おどろ)きを感じさせます。
さて、コマ回しを成立させるメカニズムは、マシーンとコマの双方(そうほう)にあります。
マシーン側に必要なのは、できる限り高速にコマを回転させることです。本体上部に取り付けたギアLが、どえらい速さで回りますね。
どれくらい速いのでしょうか？ モーターの回転と同じでしょうか？
だったら、モーターにシャフトを一本つき刺(さ)して、ギアLを付ければ済(す)む話です。
実際は、ギアの噛(か)み合わせを工夫して、回転スピードを上げています。
これを増速(ぞうそく)といいます。写真を見てください。
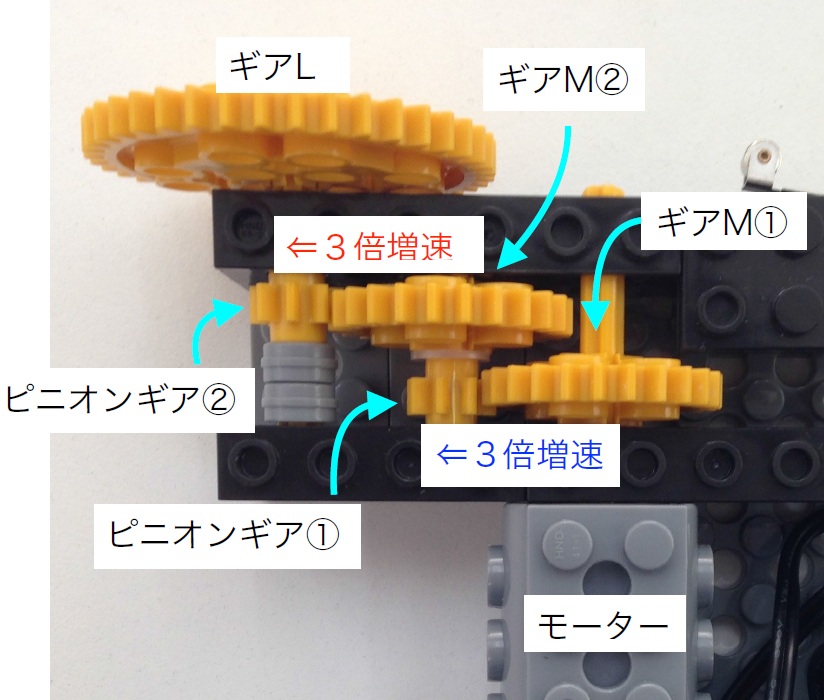〔 モーター＝ギアM① ⇒ ピニオンギア①＝ギアM② ⇒ ピニオンギア②＝ギアL 〕の順に回転を伝えていますね。
ここで、“＝”は、同一のシャフトに通して「一緒に回転している」ため、回転スピードが変わらないことを表しています。
一方、“⇒”は「大きいギアが小さいギアを回している」箇所(かしょ)であり、ここで回転スピードが上がるのです。
どれくらい上がるかは、ギアの歯数(はすう)の比(ひ)で決まります。歯数を(数字)で表すと、本体内部で、ギアM(24) ⇒ ピニオンギア(8)の３倍増速が２段と、
本体上部で、ギアL(40) ⇒ コマのギアM(24)の5/3(=1.666…)倍増速があります。
つまり、3×3×5/3＝15倍の増速作用があります。
ギアの組み替(か)え次第で、計算上はこれ以上の増速比を出せますが、今回の15倍速でも、モーターの回転速度は無負荷(むふか=空回り状態)時よりだいぶ遅(おそ)くなり、
「重くしたコマの加速にも少し時間がかかる」くらいマシーンの限界能力に近いですから、これ以上に欲張(よくば)っても大差ない(*1)かもしれません。
全エネルギーをコマの回転運動に使い尽(つ)くすという意味では、とてもピュアなマシーンです。
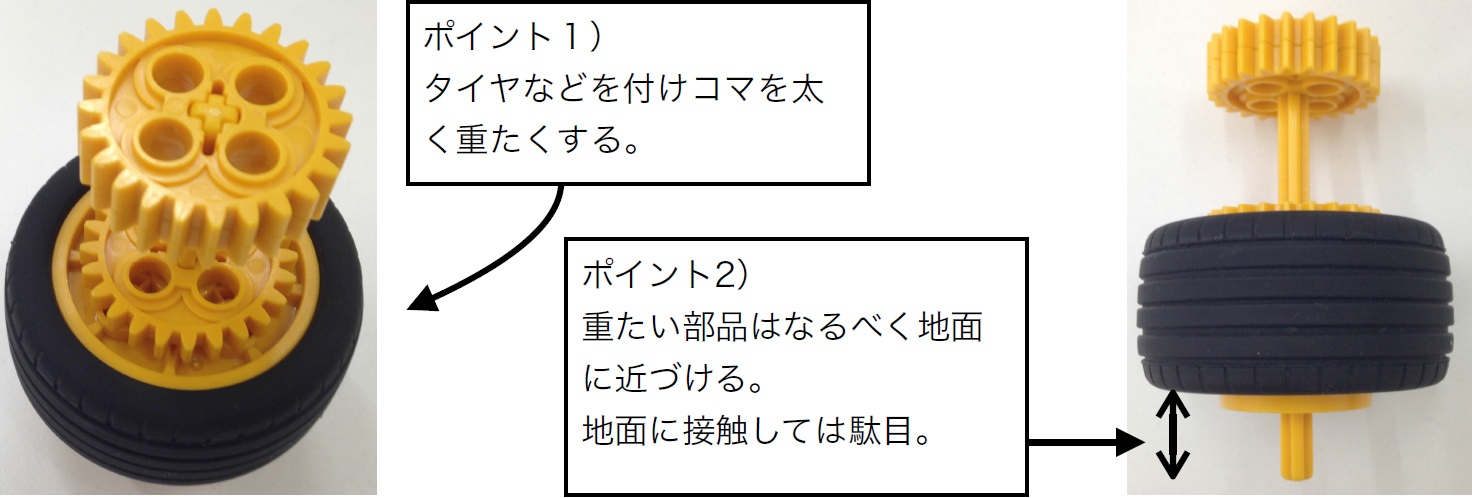コマ側に必要なのは、いかに安定して回転が長時間続く形にするかという点です。ロボットキットの中から、軸(じく)としてシャフト、回転体として円形部品(*2)を選択するという制約下(せいやくか)では、
1) コマを重く（なるべく直径を大きく、かつ外周部を重く(*3)）
2) 重心を低く（なるべく重い部品を下の方へ(*4)）
という２点をポイントとしておきますが、
あまりに重すぎると、マシーンで十分加速できなくなったり、
あまりに低すぎると、回転中に地面に接触しやすくなったりしますので、バランスを追求する根気強さが勝負を分けます。
さて、２日目の最後に、各自のコマ回し時間を競いました。地面の材質（ザラザラの机か、ツルツルの床か）にも左右されますが、上記２点を押さえたコマなら、30秒以上回り続けることができました。
各自が試行錯誤(しこうさくご)する中で、50秒を超え、ついには1分を超えるものまで登場しました。
逆に、弱かった電池をさらに消耗(しょうもう)して、最後には加速できなくなるという苦杯(くはい)をなめた人もいましたね。市販品のコマとは違って、自(みずか)ら色々と部品を組み替えて試せる点においては、遊びながら考えさせる優れた教材になったと思います。
学術的にも、コマの原理は、何年も勉強し続ける人もいるくらいとても奥深いもの。
高校物理を学んで、また改(あらた)めて興味を持ってもらえたらいいですね。
*1 限界に近いながらも、2015年5月の生徒さんが、コマ上端のギアM(24)をピニオンギア(8)に替えて、さらに3倍(トータル45倍!)の増速比を稼(かせ)いで100秒を可能にする加速方法を編(あ)み出しました。
ジェットエンジンの始動のように、加速完了まで10秒以上かけて回転音が高まるようなカッコイイもので、先生が披露すると、その方法が皆さんを虜(とりこ)にしていましたね。
2018年5月の中間教室2年生も、先生の支援を取り入れて、ギアL(40)⇒ピニオンギア(8)の５倍増速×２段＝25倍で92秒を達成し、2位の50秒を圧倒していました。理論を体現した結果であり、正に科学の勝利ですね！
*2 必ずしもタイヤ・ギアのような円形部品を使う必要はなく、回転軸（シャフト）に対して対称となるような配置（点対称）なら、他の部品でも使えます。
例えば、タイヤLのホイール穴にペグを4本挿(さ)して重くした工夫例がありました。
*3 回転エネルギーをたくさん貯(た)められるようになります。このことを物理学で「慣性(かんせい)モーメントが大きい」と言います。*4 過去には、重心を高く作ったことで不利なふらつき（歳差(さいさ)運動）を、下部に履(は)かせたホイールの縁(ふち)と地面との低摩擦な接触で抑制(よくせい)し、好記録を出した工夫例も見られました。
1.3 ＜ミドルコース『ヤジロボベエ』＞
ピンと張った紐(ひも)を伝(つた)うロボットですが、１日目はロープウェイ、２日目は一輪車でサーカスの綱渡りをするようなロボットと、形態を大きく変えます。
ここまで作り変えるテーマは、他にありません。面白いですね！
学習ポイントは“重心”です。
ロープウェイ型ロボットは、ローラーだけ紐の上に掛けて、重い本体を吊(つ)り下げていますから、重心は、見た目通り、本体の中心部にあって、支点（紐と接するローラーの最下点）より下に位置します。
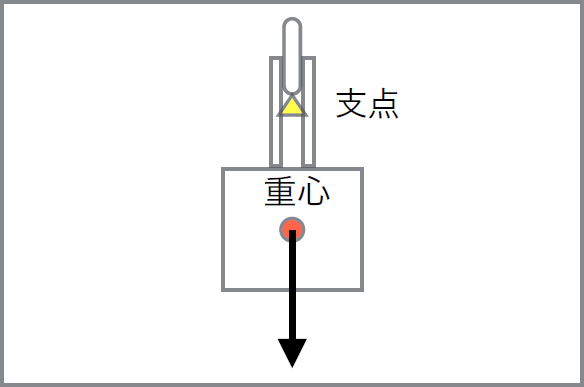重心に集中して重力が掛かると考えてよいため、（その直上の）支点も真下に引っ張られるものの、紐に引っ掛けられて（上向きの力で吊られて）いるので、安定して支えられます。ゴンドラが風に煽(あお)られて、重心が支点の真下からずれても、しばらく揺(ゆ)れるだけで、また元の安定した姿勢に収まります。
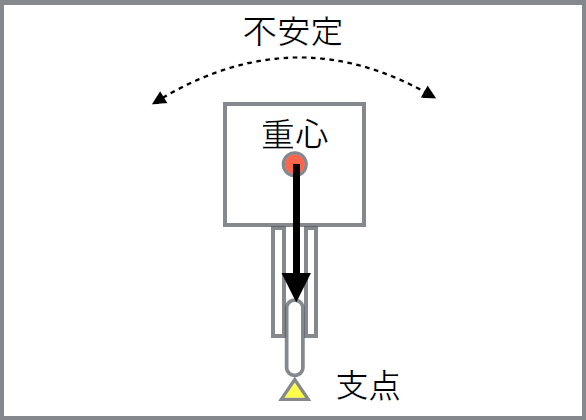ここで、このゴンドラを逆立ちさせるように、ローラーの上端を紐の上に置こうとしたら、どうなるでしょうか？支点（紐との接点）より上にきた重心が重力で引っ張られる結果、横にコロッと半回転しながら落下してしまいます。
サーカスの綱渡りもこの状態であり、本来は非常に不安定なところ、横に伸ばした両腕や長い棒を傾けつつ、上手にバランスを取っています。
このロボットに、そこまで期待できませんね。
ところが、２日目のロボット『ヤジロボベエ』は、これを見事にやってのけます。一輪車に乗った彼の重い胴体は、支点よりかなり高い位置にありそうで、逆立ちしたゴンドラ同様に不安定そうですが、なかなかどうして、バランスの取れたロボットなら、多少のロープの揺れもお構いなく、スイスイと渡ってしまいます。
なぜでしょうか？
変わったところと言えば、ハの字形をした長い棒を持っていることです。それがどうして？ 綱渡りサーカスの長い棒と同じじゃない？
いえいえ、ハの字形に垂れ下がった棒の両端に、重い電池ボックスやタイヤを取り付けているところがミソなのです。
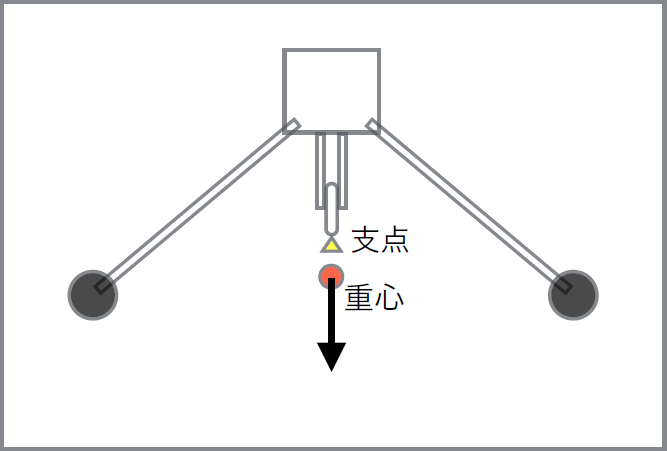これにより、ロボットの重心を支点より下に引き下げることができます。紐の真下には部品が何もないのに？ それでも構いません。
計算上、このロボットの重心は、紐の下の空中に位置することになり、これにより、彼をゴンドラ同様に安定させているのです。
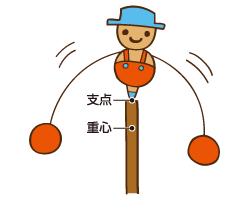
やじろべえを知っていますか？ 同じ原理です。おもりや棒の長さを調整して左右のバランスを取ることが重要ですが、それだけではありません。
一定以上に傾かず、支点もしっかり固定されているシーソーなら、左右のバランスだけ気にすればよいので、重さの代わりに支点からの長さ（座る位置）を調整してもよいのですが、足場の危(あや)ういやじろべえは、さらに、重心が支点の下にあることが必要です。
ですから、あまり棒を短くすると、重心がどんどん上がって、支点に近づくほど不安定になってしまいますので、要注意です。
皆さんのヤジロボベエは、紐の上で上手にバランスを取ることができましたか？おもりの追加や、棒の長さで調整できることは分かったと思いますが、なぜ長さの調節でもバランスが取れるのか、不思議ではありませんか？
有名な“てこの原理”ですが、おもりに働く重力（重さ）と、支点からの距離（長さ）が関係しています。
説明を簡単にするために、シーソーを使って考えてみましょう。
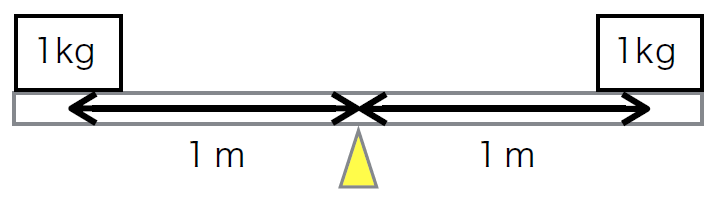図では、支点から1mの距離で、両端に1kgのおもりを置いています。この場合、左右で重さも長さも等しいので、シーソーはバランス（均衡(きんこう)状態）を取れます。
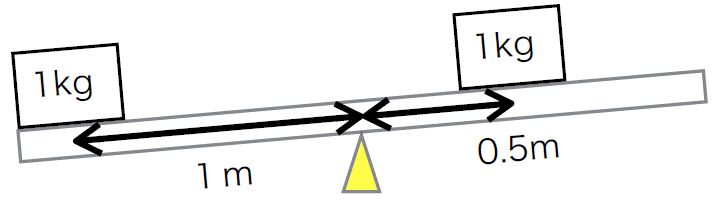次の図では、おもりの重さは変えずに、支点からの距離を右側だけ変えてみました。すると、シーソーは傾きますね。
このように、重さだけではなく、支点からおもりまでの距離によっても、支点に作用する力が変わってきます。
支点を中心に物体（シーソーの板）を回転させようとする力を回転力（トルク）と呼びます。
実は、〔 トルク ＝ 押す力(重さ) × 支点からの距離(長さ) 〕で決まります。
傾いたシーソーの支点に働くトルクを計算してみましょう。
左側のおもりによるトルク ＝ 1kg × 1m ＝ 1[kg・m] 反時計回り
右側のおもりによるトルク ＝ 1kg × 0.5m ＝ 0.5[kg・m] 時計回り
やはり、左側のトルクの方が強く、シーソーは左に傾くことが分かります。
左右のトルクを同じ（向きは逆）にすれば、シーソーはバランスを取れます。
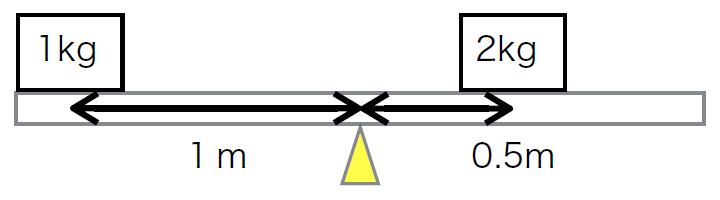最後の図ではどうでしょう。計算してみましょう。左側のおもりによるトルク ＝ 1kg × 1m ＝ 1[kg・m] 反時計回り
右側のおもりによるトルク ＝ 2kg × 0.5m ＝ 1[kg・m] 時計回り
等しくなりましたね。この場合、シーソーはバランスを取れるのです。
ヤジロボベエのバランス調整にも同じことが言えます。おもりを付け足す代わりに、棒を長く伸ばして（おもりを支点から遠ざけて）も、トルク（傾こうとする力）を増やすことができるのです。
1.4 ＜アドバンスコース『ドレミボット(2)』＞
《下記を参照下さい》
http://robocobo.sakura.ne.jp/blog/robot/adv1-1711.pdf
写真は、木琴演奏ロボットを“魔改造”して、剣道試合を繰り広げる模様。。
1.5 ＜プロ１年目コース『リンクロボット(2)』＞
モゾモゾ歩く多脚リンクロボットの２ヶ月目です。
前月の製作の過程で、曲線に富んだパーツをいくつも繋ぎ留めていくので、とても複雑に見えるリンク機構ですが、“節”（ジョイント部分）を直線で結んで考えれば、いくつかの変形する４節リンクを組み合わせた構造と捉えることができました。その一部のパーツ（中間リンクや従動リンク）を好きな方向に好きなだけ延長して、手足のような動きを作り出します(*1)。
４節リンクのうち、対向する２辺が等長の平行リンクでは、平行四辺形を保ちつつ整った変形を見せますが、
不等長になると、１辺（駆動リンク）を一定の速さで動かしていても、対向辺（従動リンク）では、角度によって異なる速さ(*2)で伝わったり、途中から逆回転したり、中間リンク(*3)と一直線に突っ張って動かなくなるか、回転方向が定まらずに「カクッ」と引っ掛かる状態（死点、特異点）になったりしました。
この死点または特異点は、どのリンクを駆動するかによって全く変わるので、駆動リンクと従動リンクの別に留意し、膠着(こうちゃく)状態を回避するよう設計することが重要なのでした。
ロボット教室で学習した、自動車や蒸気機関車のピストン式エンジン(*4)でも、車輪とピストンのどちらを駆動するかによって、引っ掛かりの有無が変わりましたね。
左右の脚を２個のモーターで独立して可変速度（正逆を含む）で駆動できるため、それぞれをベクトル（矢印）で表した作図により、合成された進行速度や回転中心（カーブの回転半径）が求まる考え方も学習しました。
あとは、手動（ラジコン式）プログラムだろうが、自動（タイマー式）プログラムだろうが、自律（センサー式）プログラムだろうが、左右それぞれのモーターに、どんな順序・条件・計算式で、どれくらいの数値（電圧）を与えればよいかという問題に落とし込めます。
最終月では、「感じて考える」自律型ロボットにバージョンアップしていきます。
*1 ミドルコース『ロボワン』でも学習した、てこクランク機構が基本原理です。
*2 ギアの増速・減速（てこの原理）と同様、力の大きさは反比例して伝わります。
つまり、
仕事[J = W・s] ＝ 力の大きさ[N] × 動いた距離[m]
が変わらないように、または、
仕事率[W = J/s] ＝ 力の大きさ[N] × 速度[m/s]
が変わらないように、エネルギーが伝わります。第3回テキストp.4～7参照。
*3 駆動リンクと従動リンクを繋ぐリンク。第3回テキストp.3～7参照。
*4 スライダークランク機構とも呼ばれます。第3回テキストp.12参照。
2. 今月の課題
＜スタートアップ(全コース)＞
特にありません
＜プライマリーコース＞
- オリジナル図形プリント
＜ベーシックコース＞
- オリジナル課題プリント（３面図＋設問）
- 上記授業内容を精読する（概ね３年生以上／低学年は補助の下で）
＜ミドルコース＞
- オリジナル課題プリント（３面図＋設問）
- 上記授業内容を精読する
＜アドバンスコース＞
- オリジナル課題プリント（見取図＋設問）
- 上記授業内容を精読する
＜プロ１年目コース＞
- 上記授業内容を精読する（該当テキストページを見ながら）
3. 今後の授業スケジュール
◆中間12/28は『中間市生涯学習センター』で開催します。
――――――――――【佐藤教室長】――――――――――
［東福間］第1・3土原則<学習ルームでこぼこ>
- 13:30～ ベーシック／プライマリ
- 15:30～ ミドル
- 17:30～ アドバンス
⇒ 12/7, 21, 1/4, 18, 2/1, 15
［中間］第2・4土原則<なかまハーモニーホール>
- 13:30～ ベーシック／プライマリ
- 15:30～ ミドル
- 17:30～ アドバンス
⇒12/14 第1回 なかまハーモニーホール3F会議室2
12/28※第2回 中間市生涯学習センター1F第1研修室
1/11, 25※, 2/8, 22
※12/28, 1/25はハーモニーホール利用不可の為、代替施設で開催します。
［小倉北］第1・3日原則<ムーブ>
- 10:30～ ベーシック／プライマリ
- 13:00～ ミドル／ロボプロ1年目
- 15:00～ アドバンス
⇒12/ 1 第1回 5F企画1・2
12/15 第2回 5F企画1・2
1/5, 19, 2/2, 16
――――――――――【中野教室長】――――――――――
［八幡東］第1・3土原則<レインボープラザ4F>
- 13:30～ ベーシック／プライマリ
- 15:30～ ミドル
- 17:30～ アドバンス
⇒ 12/7, 21, 1/4, 18, 2/1, 15
［小倉南］第2・4日原則<総合農事センター2F>
- 10:30～ ベーシック／プライマリ
- 13:00～ ミドル（／ロボプロ1年目）
- 15:00～ アドバンス
⇒ 12/8, 22, 1/12, 26, 2/9, 23
4. お知らせ
1) 標準キット用バッグ／ケース リニューアル品の斡旋収納性・強度などが改良されました。
http://robocobo.sakura.ne.jp/blog/goods/newBagCase.pdf
1/19(日)まで特別価格で斡旋します。ご希望の方はメールにて承ります。
・標準バッグ 3,500円⇒2,500円(税別)
・標準ケース 1,000円⇒ 700円(税別)
セット購入がお奨めです。お代はお引落しで頂戴します。
2) 宿題プリントA4化と各自印刷のお願い[再掲]
下記理由により、全員配布しておりましたA3図面用紙の全員配布を廃止し、
段階的にA4化と各自印刷へ移行したく、ご理解・ご協力お願い申し上げます。
【廃止理由】
- 本部からのA3図面用紙の支給廃止
- 宿題の(任意)提出率に鑑みた、紙資源の節約
- プリント・解答の迅速な開示と、支給洩れの解決
【移行措置】
- 12月までA4化したプリントを全員配布します
- 来年1月から月報等に記したプリントを各自印刷して頂きます
3) IchigoJam初級ミニゲーム『ネコにコバン』終了
プレイヤー(猫)を操作して、時間内になるべく多くの小判を集めるアクションゲームをプログラミングしました。
最後は、景品のドータボード（7セグ数字LED基板）を懸けて、特別に開発(?)された『ネコにコバン Final Edition』でスコアを競い合って盛り上がりました。
次回2/11(火・祝) 開催予定の講座をお楽しみに。（詳細は1月報でご案内します）
4) 10月課題 高得点者 []内は教室と学年
◆プライマリ【14名平均 図形3.8】
5点…早野(冴)[東福間 年長], 神崎[中間1], 仲井[中間2], 柴田[小倉北2]
◆ベーシック【17名平均 図面3.6＋設問2.1＝5.8】
10点…なし
9点…千葉[中間4], 藤津[中間3], 阿部[八幡東3], 原[小倉南3]
8点…米山[小倉北3]
7点…なし
◆ミドル【11名平均 図面2.2＋設問2.0＝4.2】
10点…なし
9点…なし
8点…なし
7点…中村[東福間4]
6点…重藤[八幡東8], 下木[八幡東4]
東福間・中間・小倉北教室 佐藤 / 八幡東・小倉南教室 中野
